Как ничто стало нечто и почему это так важно?

Продолжение. Начало см. «Наука и жизнь» № 4, 2023 г., стр. 81.
Изобретение нуля
Отсутствие нуля у древних греков, создавших великолепную геометрию, которой мы пользуемся и поныне, на первый взгляд может показаться удивительным. Но это было связано уже не с трудностью осознания нуля (с абстрактным мышлением у греков всё было неплохо), а с их научно-философскими взглядами. Они строили свою алгебру на основе геометрии, где всё опиралось на построение. Числа представлялись отрезками, полученными повторением отрезка, принятого за единицу, или с помощью геометрических фигур. Мы до сих пор, следуя древним грекам, используем для второй и третьей степеней числа названия «квадрат» и «куб». Такой подход, с одной стороны, позволил им добиться больших успехов, а с другой, сильно ограничил развитие математики. Нулю в ней места не было, ведь его невозможно построить. Более того, греческие математики не считали числом даже единицу! Для них, как написано у Евклида, числом было лишь множество, составляемое из единиц. Их взгляды настолько глубоко укоренились в европейской науке, что споры о том, является ли единица числом, продолжались до XVII века. С этой точки зрения нуль как число тем более не мог существовать.
Противоречил нуль и греческой философии. Не углубляясь, упомянем лишь пифагорейское «вещи суть числа» и утверждение Аристотеля, что «природа не терпит пустоты». А ведь труды последнего во многом определили средневековые европейские воззрения. В результате научные взгляды греков не только не позволили ввести нуль им самим, но впоследствии долго мешали введению нуля в европейскую математику, тормозя её развитие. Неопределённый смысл нуля приводил к философским, а в Средние века даже к религиозным дискуссиям о его природе и существовании.
А ведь всё могло быть иначе. Греческие астрономы, взявшие на вооружение вавилонское наследие, ещё до нашей эры использовали знак нуля в виде кружка с волнистой чертой сверху Õ в шестидесятеричных числах. Однако, закончив расчёты, они опять переводили числа в родную алфавитную систему. Такой нуль часто применял Клавдий Птолемей в своём «Альмагесте» (около 140 года) для выражения именно нулевого значения. Он был уже совсем близок к современному нулю, но последний шаг — признать это обозначение цифрой — Птолемей почему-то так и не сделал. Видимо, любовь к мудрости — философия — здесь всё же победила математику. Тут греки, что называется, перемудрили.
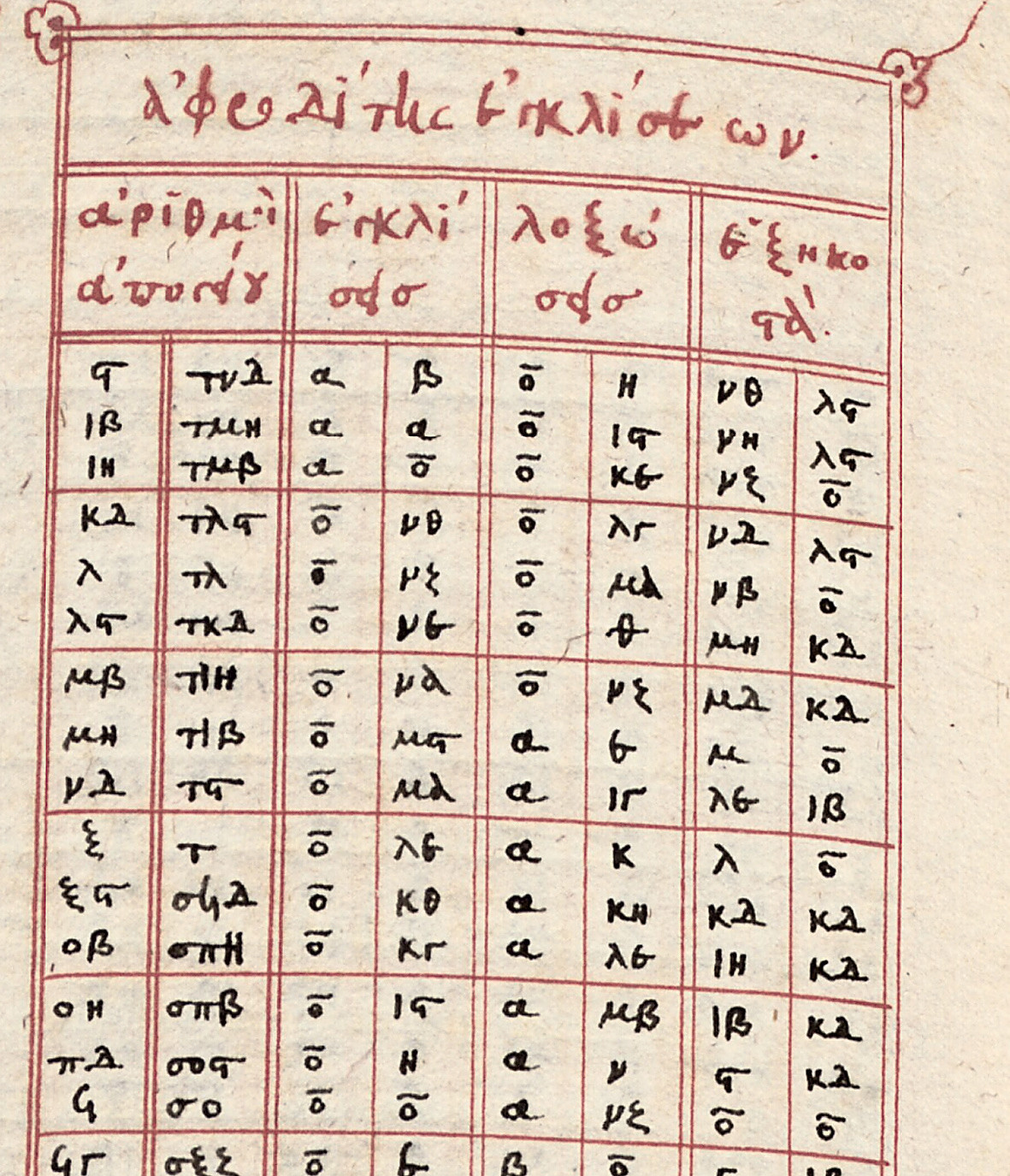
Традиционно считается, что «птолемеевский нуль» представляет собой греческую букву омикрон, первую букву слова «ουδεν» — «ничего». Но некоторые исследователи полагают его специально изобретённым символом, поскольку в ранних вариантах он мало напоминает букву «ο»:

Черта сверху, которая обозначает цифру, здесь гораздо длиннее кружка и, в свою очередь, оканчивается кружками... Впрочем, альтернативного объяснения появления в символе именно кружка эти исследователи дать не могут. Есть любопытная гипотеза, что форма нуля связана со счётом с помощью камешков на доске, посыпанной песком или пылью, которую называли абаком. Когда означавший цифру камешек убирали, на его месте оставалась ямка, похожая на букву «ο». Так это или иначе, но птолемеевское написание нуля, возможно, сыграло свою роль в обретении им современной формы.

Оставим на время зашедшую в «нулевой» тупик Европу и переместимся в Индию, где был сделан решающий вклад в изобретение нуля. Сам этот факт сейчас уже никем не оспаривается, хотя его детали до сих пор служат предметом для дискуссий. Индийские историки, как истинные патриоты, считают, что позиционная система счисления возникла в их стране без всякого влияния извне. Их оппоненты из других стран придерживаются мнения, что это влияние всё же было. Однако надёжных доказательств нет ни у тех ни у других, и, вероятно, мы их так никогда и не получим. Математические трактаты того времени писались на очень непрочном материале вроде пальмовых листьев или бересты, который долго не хранился в тёплом и влажном климате Индии. Поэтому дошедшие до нас сведения почерпнуты из более поздних копий или цитат.
Тем не менее историки обнаружили много свидетельств того, что после индийского похода Александра Македонского (327—326 годы до н. э.), принёсшего на эту землю эллинистическую культуру, шумерско-греческие астрономические тексты оказали огромное влияние на индийскую астрономию. Индийские учёные заимствовали оттуда идеи и даже выражения, так почему же они не могли, отталкиваясь от идеи вавилонян, создать позиционную систему? Правда, уже десятичную с собственными цифрами, которые стали предками цифр, используемых в настоящее время. Мы часто называем их арабскими цифрами, поскольку в Европу они попали через арабские страны. Впрочем, было или нет влияние, не так уж и важно. Ни одна культура не сможет позаимствовать у другой сложную идею, если она к ней ещё внутренне не готова.
