Пути и маршруты
Мосты Кёнигсберга и Эйлеров путь
Знаете ли вы, что подтолкнуло английского математика Леонарда Эйлера к созданию основ теории графов? Ответ может показаться неожиданным: поиск решения задачи, связанной с мостами города Кёнигсберга.
Кёнигсберг (ныне Калининград) возник в XIII веке как три независимых поселения на островах и берегах реки Преголи. Он расположен между Польшей и Литвой на берегу Балтийского моря. Постепенно между поселениями налаживались активные торговые связи (хотя не обходилось и без военных конфликтов), поэтому возникла необходимость более тесного взаимодействия. В XIV веке началось строительство сразу нескольких мостов, и к концу XV столетия их было уже семь. Во многом благодаря мостам три независимых поселения слились в один большой город. Мосты стали его достопримечательностью, на них устраивали празднования, карнавалы, религиозные шествия.
Однажды местный житель, имени которого мы не знаем, задался вопросом: можно ли совершить прогулку по всему городу, пройдя по каждому мосту ровно один раз? Задача приобрела большую популярность, её задавали прибывшим в Кёнигсберг туристам и обязательно говорили о том, что такой маршрут есть — нужно только очень постараться его найти. Горожане, конечно, знали, что побывать во всех частях города, пройдя по каждому мосту всего один раз, невозможно. В этом легко было убедиться, просто перебирая разные маршруты.

В 1730 году задачей про мосты Кёнигсберга заинтересовался Леонард Эйлер (1707—1783), который решил её обобщить и найти ответ на вопрос: при каком условии мосты и острова образуют такую конфигурацию, что посетить каждый мост всего один раз можно, а при каком — нельзя? Эйлер задумался: о каком, собственно, математическом объекте идёт речь в этой задаче? Подходящих объектов, описывающих подобные ситуации, он не знал и придумал новый — граф.
Что такое граф? Это набор точек (они называются вершинами графа), некоторые из которых соединены линиями (не обязательно прямолинейными отрезками), называемыми рёбрами графа. Отметим, что геометрические свойства этих линий — прямые они или кривые, пересекаются или нет — не влияют на свойства графа. Важно лишь то, какие именно вершины с какими соединены.
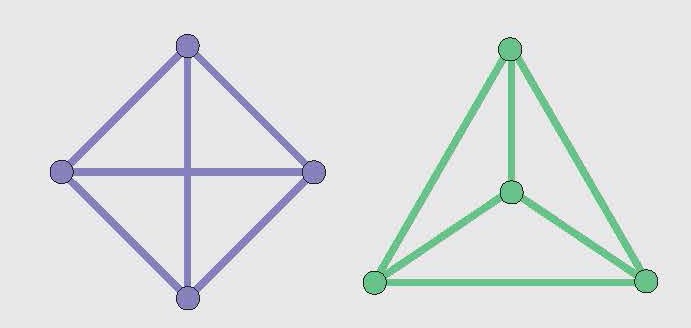
Приведём наглядный пример. Представим себе нескольких человек — они будут вершинами графа. Если двое из них знакомы, будем считать, что их связывает ребро. Изображать граф можно разными способами хотя бы потому, что люди, например, могут находиться в разных местах. Граф будет получаться один и тот же, даже если картинка меняется. Например, если четыре человека знакомы друг с другом, то граф, соответствующий этой ситуации, можно изобразить разными способами: как квадрат с диагоналями и как треугольник с точкой внутри (рисунок слева). Картинки получаются совершенно разными, но граф, изображённый на них, один и тот же. Это полный граф с четырьмя вершинами (полными называются графы, в которых присутствуют все возможные рёбра).
Другой пример графа, с которым знакомо большинство читателей, — карта авиалиний. Вершины его — города, а рёбра — рейсы некоторой связывающей их авиакомпании. Такой граф обычно представлен на её сайте или в рекламном буклете. По карте легко узнать, какими маршрутами можно долететь из одного города в другой.
Но вернёмся к решению задачи о мостах. Эйлер представил карту мостов в виде графа: рёбра — мосты, а острова и берега — вершины. Правда, некоторые пары вершин получившегося графа оказались соединены двумя рёбрами (такие рёбра называются кратными), но это не важно. Для каждой вершины — вслед за Эйлером — посчитаем количество выходящих из неё рёбер. Такое число называется степенью вершины. У вершин B, C и D степень равна трём, а у вершины A — пяти.
