Бери ниже

Как математики сдвинули с мертвой точки диагональное число Рамсея

Фёдор Петров

В комбинаторике прямо сейчас происходит много весьма интересных событий, это одна из самых бурно развивающихся областей математики. Но среди них отдельно выделяется новая работа Марсело Кампоса, Саймона Гриффитса, Роберта Морриса (Рио-де-Жанейро) и Джулиана Сахасрабуде (Кембридж), посвященная оценке чисел Рамсея. В чем с этими числами проблема и как ее недавно решили, рассказывает математик Фёдор Петров, профессор СПбГУ и ведущий научный сотрудник ПОМИ РАН.

Числа Рамсея

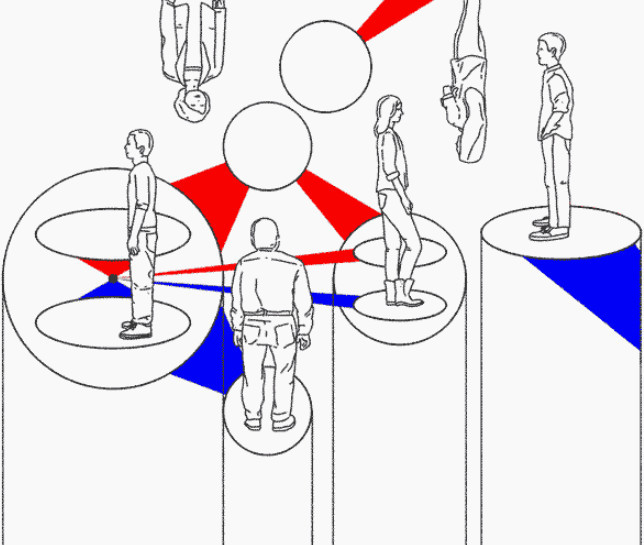
Чтобы определить числа Рамсея, начнем с задачи, которую решают на школьных математических кружках: докажите, что из любых шести людей найдутся трое попарно знакомых или трое попарно незнакомых (будем считать, что знакомство взаимно).

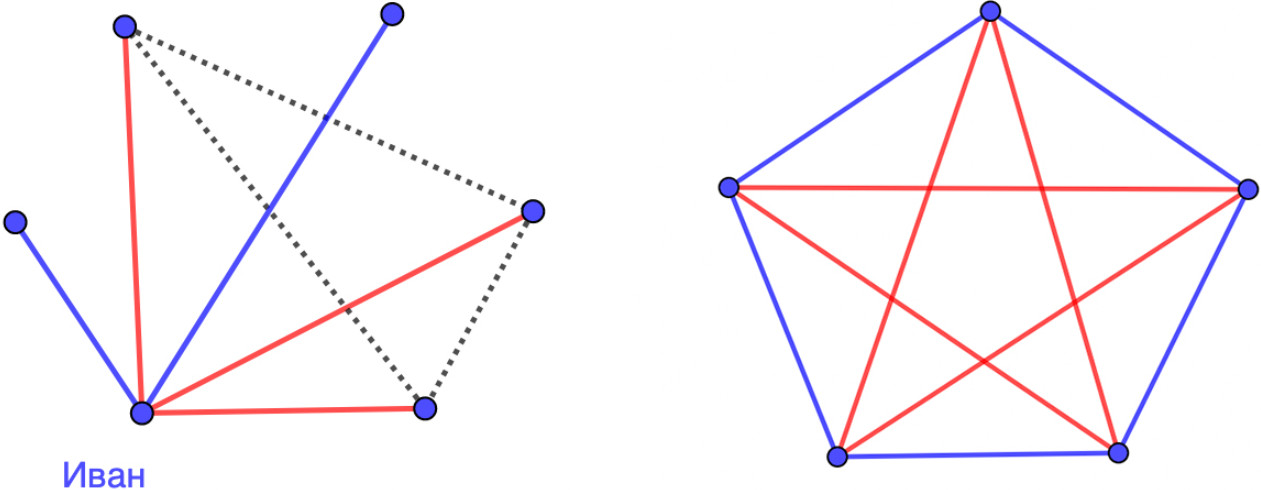
Возьмем любого из шестерых — назовем его Иваном. Предположим, что он знает хотя бы троих из оставшихся. Если среди этих троих есть двое знакомых, они образуют искомую тройку (попарно знакомых) с Иваном, если нет — то тройку попарно незнакомых между собой. Если же Иван знает не более двоих из оставшихся, то у него есть трое незнакомых, и для них работает аналогичное рассуждение. Также легко видеть, что в компании из пяти человек может уже не найтись троих попарно знакомых или попарно незнакомых: поставим пятерых изначально незнакомых людей по кругу и познакомим соседей.

На языке теории графов это утверждение формулируется так: если есть граф с шестью вершинами (это люди), ребра которого раскрашены в красный и синий цвета (знакомство и незнакомство соответственно), то найдутся три вершины, соединенные ребрами одного цвета. А для графа с пятью вершинами такой тройки может и не быть.

Графы для R(3,3) = 6 и R(3,3) = 5. john doe

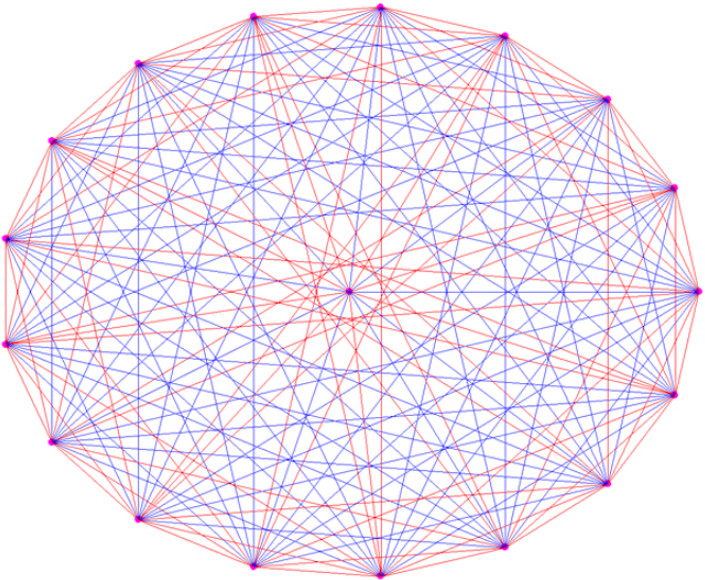
А если мы хотим найти в какой-нибудь группе больше людей, которые или каждый с каждым знакомы, или каждый с каждым не знакомы? Верно ли, что какие бы значения n и k мы не взяли, в достаточно большой компании найдутся или n попарно знакомых, или k попарно незнакомых людей? Да, верно: это доказал английский математик Фрэнк Пламптон Рамсей в 1930 году. Наименьший размер компании, заведомо удовлетворяющей этому условию, обозначается R(n,k) и называется числом Рамсея. Выше мы установили, что R(3,3)=6.

У этого графа R(4,4) = 18 вершин.
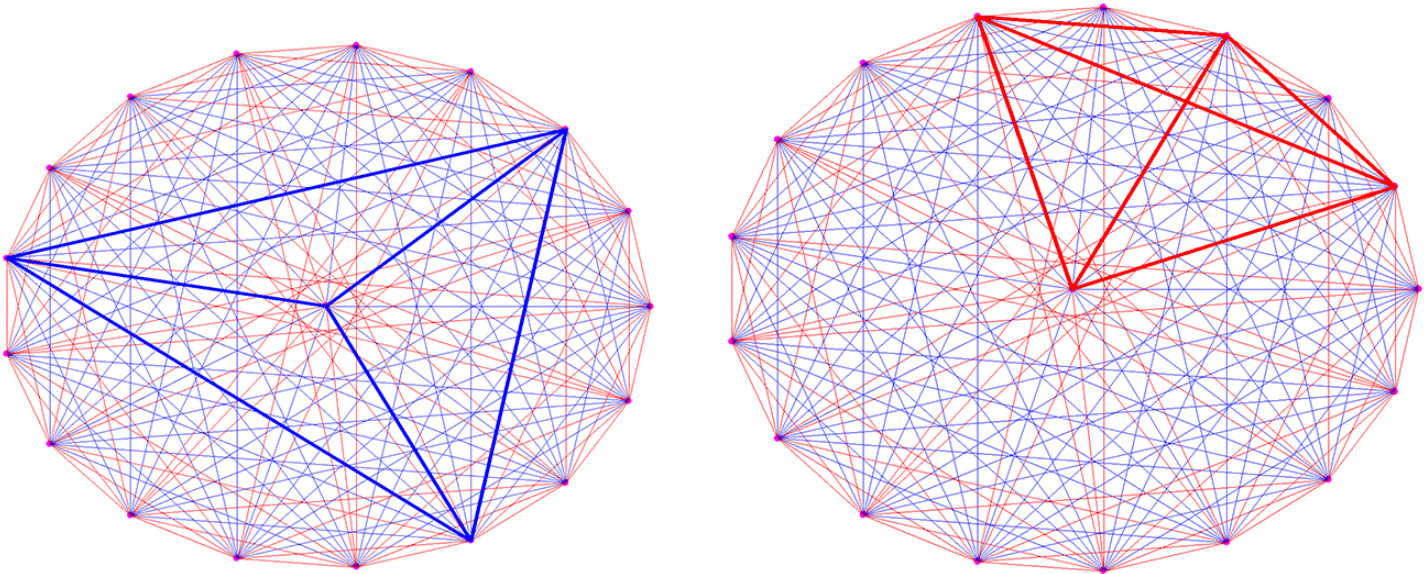
Следовательно, здесь найдутся 4 вершины соединенные либо только красными, либо только синими ребрами. Попробуйте найти такую четверку! john doe

Таких четверок в этом графе несколько, вот два из них. john doe

Считать числа Рамсея очень трудно. Известно, что:

R(4,3)=9,
R(4,4)=18,
R(3,5)=14,
R(4,5)=25 (это сложно).

А вот R(5,5) уже неизвестно. Известно только, что 43⩽R(5,5)⩽48.

Как говорил математик Пол Эрдёш больше 30 лет назад, если на Землю нападут пришельцы и потребуют в течение года назвать