Как абстрактная математика помогает конкретной физике
Иногда на первый взгляд совершенно абстрактные математические теории помогают физикам-теоретикам понять, как устроен наш мир.

В год окончания Первой мировой войны двое немецких математиков геттингенской выучки опубликовали работы, имеющие огромное значение для теоретической физики. Одна из самых блестящих алгебраистов XX века Эмми Нётер представила доказательства двух знаменитых ныне теорем, связывающих законы сохранения различных величин (энергии, импульса, углового момента, заряда и т. д.) с симметриями уравнений, описывающих физическую систему.
Эти теоремы стали мощным и универсальным средством выявления подобных законов в ньютоновской и релятивистской механиках, в теории тяготения, электродинамике, квантовой теории поля и физике элементарных частиц.
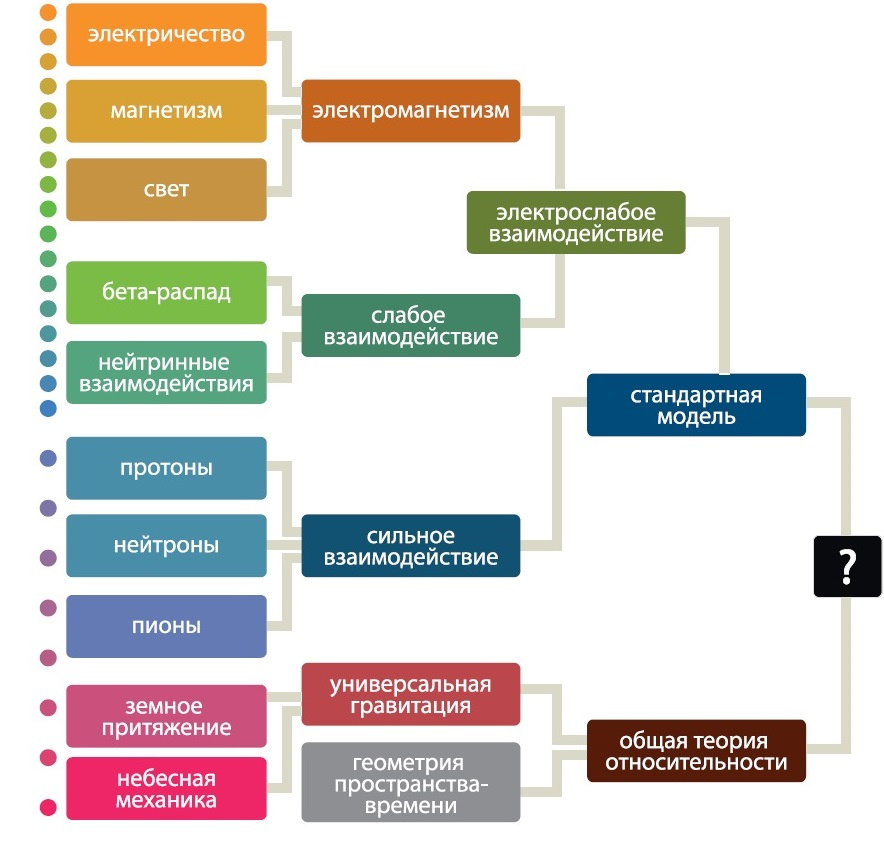
Статья Германа Вейля «Гравитация и электричество», опубликованная не в Геттингене, а в Берлине, известна гораздо меньше. Между тем она и ее продолжение, вышедшее годом позже, положили начало чрезвычайно эффективному подходу к конструированию теорий микромира, который сформировался уже во второй половине XX века. С его помощью была создана объединенная теория трех фундаментальных взаимодействий, сильного, слабого и электромагнитного, которую назвали Стандартной моделью.

От сил к потенциалам
Как обычно и бывает, у Вейля имелись предшественники. В начале XIX века работы нескольких математиков, прежде всего Гаусса и Пуассона, преобразовали математический аппарат ньютоновской теории тяготения. В новой интерпретации она предстала как силовое поле, пронизывающее Вселенную. Это поле стали описывать гравитационным потенциалом — скалярной функцией, зависящей от пространственных координат, но не от времени. При этом сила тяготения в любой точке полностью определяется тем, насколько резко изменяется вблизи нее этот потенциал (то есть его градиентом).
Это нововведение обогатило математический аппарат небесной механики и других разделов физики, где приходится иметь дело с тяготением, но ввело в описание гравитации некую неопределенность. В законе Ньютона фигурируют силы тяготения, которые можно измерять непосредственно, и определяются они однозначно (в выбранной системе единиц). А вот значения гравитационного потенциала можно изменить на любую постоянную величину — градиент останется тем же. В те времена это выглядело тривиальным следствием математического формализма, не имеющим отношения к реальной физике.
Столетием позже таким же образом переписали классическую электродинамику. В первоначальной форме она была представлена уравнениями Максвелла, куда входят измеряемые на опыте напряженности электрического и магнитного поля. Эти уравнения тоже удобно выразить через потенциал, только более сложный, чем у ньютоновской гравитации (помимо скалярной части, в него входит вектор, определяющий величину магнитного поля).
Уравнения электродинамики в такой записи выглядят очень элегантно и естественно встраиваются в пространство-время специальной теории относительности. Однако они становятся неоднозначными, поскольку одному и тому же полю могут соответствовать разные потенциалы. Например, к векторному потенциалу можно добавить любой постоянный вектор, а к скалярному — любое число.
Более того, эти добавки могут меняться и в пространстве, и во времени, лишь бы они были правильно связаны друг с другом, так что произвол в выборе электромагнитных потенциалов существенно больше, чем в случае ньютоновской гравитации. Физики и математики начала прошлого века прекрасно видели эту неоднозначность, но, как и предшественники, не придавали ей особого значения.
Калибровочные преобразования
Это свойство электромагнитных потенциалов имеет глубокий физический смысл. Их взаимные изменения компенсируют друг друга точно таким образом, чтобы сохранить в прежнем виде уравнения Максвелла. Неоднозначность выбора фактически отражает неразрывную связь между электричеством и магнетизмом.
Преобразования потенциалов, не меняющих уравнений электромагнитного поля, называют калибровочными (этот термин тоже восходит к статьям Вейля) — как говорят физики, эти уравнения инвариантны относительно калибровочных преобразований. В квантовой электродинамике такая инвариантность, в соответствии с теоремой Нётер, влечет за собой закон сохранения электрического заряда. Таким образом, калибровочная инвариантность, несмотря на свой вроде бы формальный характер, открывает возможность заключений, имеющих прямой физический смысл!
И не только в отношении электромагнетизма. Принцип эквивалентности, на котором базируется общая теория относительности (ОТО), утверждает, что поле тяготения вызывает такие же физические эффекты, как и ускорение. Если недалеко от звездолета с работающим двигателем поместить тяготеющие массы, то в принципе можно полностью скомпенсировать импульсы двигателя и создать в кабине зону невесомости. Такая компенсация ускорений посредством переменного гравитационного потенциала аналогична взаимной компенсации изменений потенциалов электромагнитного поля. Это наводит на мысль, что уравнения ОТО должны подчиняться какому-то аналогу калибровочных преобразований.
