Гравитация – это притяжение или отталкивание?

На первый взгляд кажется, что это глупый вопрос, потому что давно было выяснено, что массивные тела притягивают друг друга, и про закон притяжения Ньютона нам всем рассказывают в школе. Земля вращается вокруг Солнца, Луна вокруг Земли, множество спутников... и все это вращается под действием силы гравитационного притяжения. До какого-то момента это устраивало всех, но когда появились новые наблюдения, то физики Ньютона стало не хватать для их объяснения и в дело вступила Теория относительности Альберта Эйнштейна.
Старина Эйнштейн
Эйнштейн решил добавить к понятию трехмерного евклидова пространства четвертое измерение – время, назвал все это пространством-временем, и в результате обычное и всем нам привычное трехмерное евклидово пространство стало метрикой Минковского (Лоренца), а сила гравитационного притяжения переросла в изменение геометрии этой метрики под действием гравитационных объектов.
В метрике Минковского нет ничего сложного – это такое же трехмерное пространство, которое всем известно со школы, но к которому в качестве еще одной координаты добавили время. Формулы при этом сильно усложнились, но мы не будем тут вдаваться в высшую математику, а скажем только, что это позволило искривляться самому пространству. Все мы много раз видели модель этого изменения под названием «гравитационная воронка».
С одной стороны, это позволило объяснить некоторые явления, которые не могла объяснить теория Ньютона, например, отклонение света, у которого нет массы покоя, гравитационным полем массивных объектов.
С другой – устранило неразрешимое физическое противоречие, возникающее при объяснении гравитации как силы, т.к. сила подразумевает расход энергии, а никакая энергия тела не тратится на притяжение других тел.
В Теории относительности тела в гравитационном поле стали двигаться по прямой, но по искривленному пространству – по его геодезическим линиям, которые отмечают искривление пространства, а при прямолинейном движении по инерции нет ускорения, и энергия не затрачивается, оставаясь постоянной.
Казалось бы, теперь «все в шоколаде» – ничего не понятно, но вроде работает. Однако не тут-то было. Для описания определенных случаев пришлось модифицировать метрику, и в итоге сейчас мы имеем минимум три (!) общепринятых метрики пространства Минковского, метрику Шварцшильда и еще множество специальных вариантов описания одного и того же пространства. Все эти метрики отличаются только математическим описанием и наличием или отсутствием каких-либо констант. При этом ни одно математическое описание ни одной из метрик не является полным и не может описать поведение всех объектов в пространстве, поэтому каждый случай нужно рассматривать отдельно, подбирать соответствующие формулы и стараться не замечать влияние других объектов на результаты вычислений. Все это больше похоже на гадание и шаманство, чем на научный подход. Удивительнее всего во всем этом бардаке то, что он считается нормальным состоянием науки! По идее то, что нет единой модели, описывающей все возможные варианты поведения объектов в пространстве, говорит о том, что все это множество математической шелухи неверно, и чтобы это наглядно показать, предлагаю подойти к вопросу метрик и искривления пространства с другой стороны.

Так что же такое гравитация в представлении современных ученых?
Конечно, умными словами с путаными объяснениями можно спрятать любую чушь за стену высшей математики, и никто еще долго этого не разоблачит, но если последовательно задавать правильные вопросы, то можно обнаружить эту чушь, хоть при этом и есть риск получить в спину букварем со словами «невежда». Но когда настоящего исследователя это останавливало?
Начнем, пожалуй, с уточнения, каким именно образом движутся тела в гравитационном поле, по современным представлениям:
«В стандартном подходе Общей теории относительности (ОТО) гравитация рассматривается изначально не как силовое взаимодействие, а как проявление искривления пространства-времени. Таким образом, в ОТО гравитация интерпретируется как геометрический эффект, причем пространство-время рассматривается в рамках неевклидовой римановой (точнее псевдо-римановой) геометрии. Гравитационное поле (обобщение ньютоновского гравитационного потенциала), иногда называемое также полем тяготения, в ОТО отождествляется с тензорным метрическим полем – метрикой четырехмерного пространства-времени, а напряженность гравитационного поля – с аффинной связностью пространства-времени, определяемой метрикой».
Мало что понятно, но зато как звучит: в ОТО (гравитация) отождествляется с тензорным метрическим полем – метрикой четырехмерного пространства-времени, а напряженность гравитационного поля – с аффинной связностью пространства-времени, определяемой метрикой! Прямо симфония какая-то! И это только в «стандартном подходе». Я даже боюсь спрашивать, что будет в нестандартном...
Это цитата из Википедии, и она приведена тут именно для того, чтобы показать, насколько все в физике пытаются запутать и усложнить, чтоб только специалисты могли понять, о чем тут написано, а все остальные верили на слово и не спорили с общепринятым авторитетным мнением.
Для простого обывателя существует и более простое объяснение. Можете представить себе воронку? Так вот Солнце создает вокруг себя такую же воронку в пространстве, а планеты просто летают по ее стенкам по геодезическим линиям, прямо как на рисунке выше. И еще пример с батутом постоянно приводят, в центр которого кладут камень и кидают шарики, которые кружатся в воронке, а потом падают в нее. В этих примерах все наглядно и понятно, что сам камень шарики не притягивает, но так ли верны эти модели и примеры для объяснения гравитации?
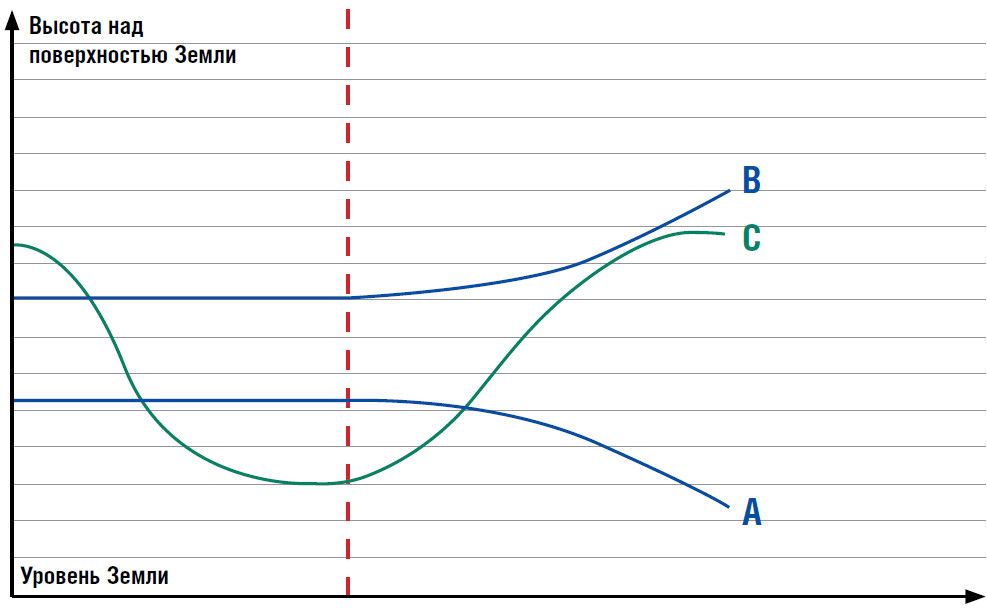
Давайте попробуем рассмотреть такую модель чуть подробнее. Возьмем эту воронку с ее геодезическими линиями и распрямим, чтобы нам было лучше видно и понятно, как именно движутся объекты в ней. Нарисуем небольшой график: по оси Х находится уровень Земли, а по оси У откладываем высоту над поверхностью Земли. Линии – это траектории спутников на разных высотах и скоростях над Землей.
