О суммах квадратов и кубов
История, о которой пойдёт речь, начинается с теоремы Пифагора, а заканчивается одним математическим открытием, сделанным в сентябре 2019 года. Точнее сказать, эта история ещё не окончена…
Пифагоровы тройки
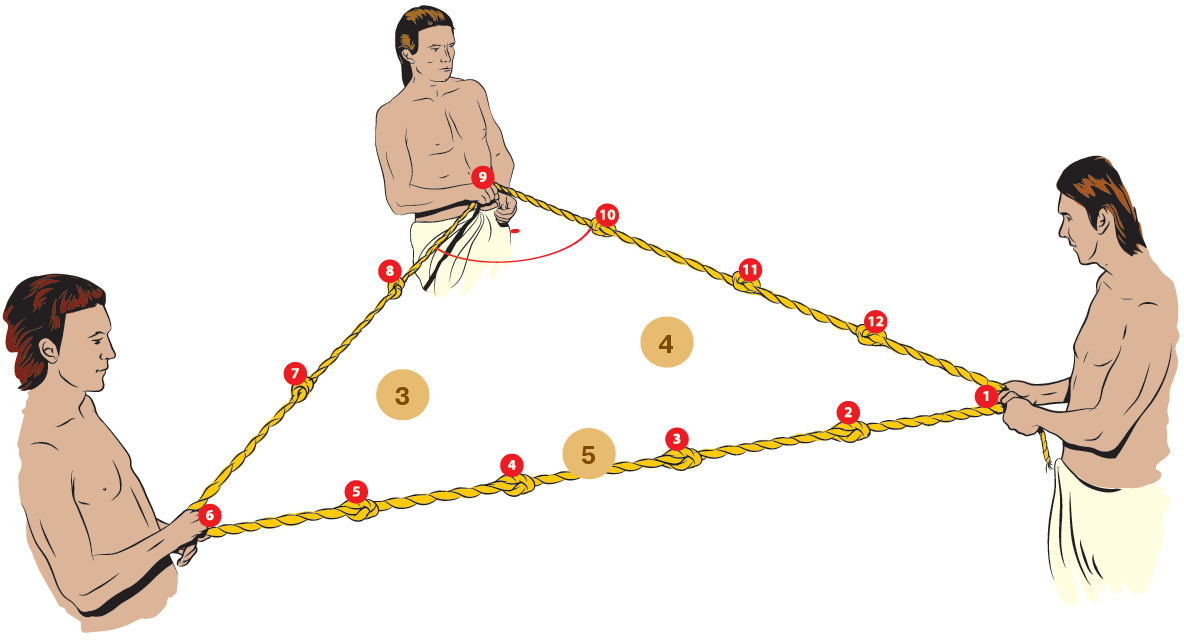
Теорема Пифагора, как известно, гласит: сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы. Прямоугольный треугольник с катетами 3 и 4 и гипотенузой 5 известен с давних времён. Ещё в Древнем Египте строители пирамид использовали для построения прямых углов верёвку с узлами, которые делили её на 12 равных частей. Задача о том, существуют ли другие тройки натуральных чисел, в которых квадрат одного числа равен сумме квадратов двух других, интересовала математиков и в Египте, и в Вавилоне, и в Греции. Сейчас такие тройки принято называть пифагоровыми, разумеется, в честь теоремы Пифагора (древнегреческий математик жил с 570 по 495 год до н. э.), но известны они были задолго до него. Глиняная табличка, содержащая 15 пифагоровых троек, которую археологии называют Plimpton 322, была изготовлена примерно в 1800 году до н. э.
Существует ли бесконечно много пифагоровых троек или их число конечно? Ответить на этот вопрос не сложно. Посмотрим на равенство A2 + (2A + 1) = = (A + 1)2. Если число 2А+1 окажется квадратом (а это может быть любой нечётный квадрат), то мы будем иметь пифагорову тройку. Так получаются равенства 122 + 52 = 132 и 242 + 72 = 252 и, понятное дело, бесконечно много других.

В книге «Начала» Евклида приведена общая формула, позволяющая находить всевозможные пифагоровы тройки. Нужно взять пару взаимно простых (то есть не имеющих никакого общего делителя, кроме единицы) чисел m и n (при условии, что m > n), и тогда тройка натуральных чисел m2 − n2, 2mn, m2 + n2 всегда будет пифагоровой. Можете проверить. Если точнее, получится примитивная пифагорова тройка, то есть такая, в которой у чисел нет общего делителя, кроме единицы. Самое важное то, что верно и обратное утверждение: любая примитивная пифагорова тройка представляется в таком виде для некоторых взаимно простых m и n. Доказать это не слишком просто, но вы можете попробовать.
Суммы двух квадратов
Обобщать задачу о пифагоровых тройках можно в разных направлениях. Например, есть такое понятие, как пифагоровы четвёрки: четыре натуральных числа, таких, что квадрат одного равен сумме квадратов трёх остальных. Но зададимся другим вопросом: какие числа можно представить в виде суммы квадратов двух натуральных чисел?
Начнём с естественного вопроса: может быть, в виде суммы двух квадратов представляется просто любое число? Оказывается, нет. Убедиться в этом нам помогут остатки от деления на 4.
Сначала заметим, что если возвести в квадрат чётное число, то результат будет обязательно делиться на 4. Действительно: 2k · 2k - 4k2. А что будет, если возвести в квадрат нечётное число? Посмотрим:
(2k+1)2 - (2k+1) · (2k + 1) - 4k2 + 4k + 1 - 4(k2 + k) + 1.
Итак, мы видим, что квадрат нечётного числа от деления на 4 всегда даёт остаток 1. Два наших наблюдения позволяют сделать очень полезный вывод: квадраты натуральных чисел от деления на 4 могут давать только остатки 0 или 1.
Этот факт можно было доказать и иначе, воспользовавшись тем, что остаток произведения можно найти, если перемножить остатки множителей. Использовать полученный результат нужно аккуратно: нельзя говорить, что остаток произведения равен произведению остатков (например, если два числа дают остатки 2 и 3 от деления на 4, то остаток произведения вовсе не 6, а 2), но, перемножив остатки множителей, мы узнаем остаток произведения.

Так или иначе, но мы поняли, что квадраты чисел дают не всевозможные остатки от деления на 4. Теперь рассмотрим сумму двух квадратов. С точки зрения остатков, от деления на 4 мы имеем три случая: 0 + 0, 0 + 1, 1 + 1. То есть получается, что сумма двух квадратов не может давать остаток 3 от деления на 4. А это значит, что есть бесконечно много чисел, не являющихся суммой двух квадратов.
Ну, а какие же числа представимы в виде суммы двух квадратов? Найти ответ на такой вопрос гораздо сложнее, и, как оказалось, он зависит от разложения числа на простые множители. В 1640 году знаменитый французский математик Пьер Ферма в письме своему соотечественнику математику Марену Мерсенну сообщил об одном своём новом открытии: любое простое число, дающее остаток 1 от деления на 4, представимо в виде суммы двух квадратов. Например, 5 - 1
