Игра в конфигурации: читайте о новой головоломке
Предлагаем вам вариант еще одной новой и увлекательной игры, которая подойдет как детям, так и взрослым. На первый взгляд, она представляет собой типичную головоломку с переменными начальными условиями типа кубика Рубика, судоку или пасьянса. Однако ее возможности значительно шире.

Игра в конфигурации может использоваться как конструктор для разнообразных красивых конфигураций – аналогично игре (точнее, клеточному автомату) “Жизнь”, – а также для создания интересных математических задач.
Правила игры очень просты. На “бесконечном” листе бумаги в клетку задается произвольная начальная конфигурация из конечного числа крестиков, которую назовем затравкой. Пример затравки представлен на рис. 1.
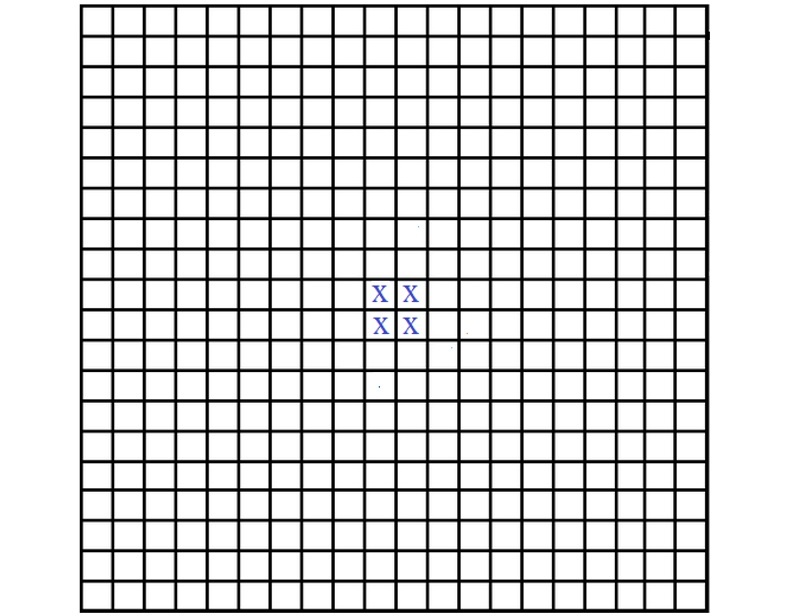
К затравке последовательно добавляются новые крестики в соответствии со следующими двумя правилами.
- Каждый выставляемый крестик должен образовывать с уже выставленными хотя бы один ряд из трех рядом стоящих крестиков по вертикали, горизонтали или диагонали. Из этого правила следует, что нельзя выставлять изолированный крестик, а также выстраивать ряд, состоящий лишь из двух рядом стоящих крестиков.
- Запрещается ставить крестик, если он при этом образует с уже выставленными хотя бы один ряд более чем из трех рядом стоящих крестиков. Эти правила иллюстрируются на рис. 2.
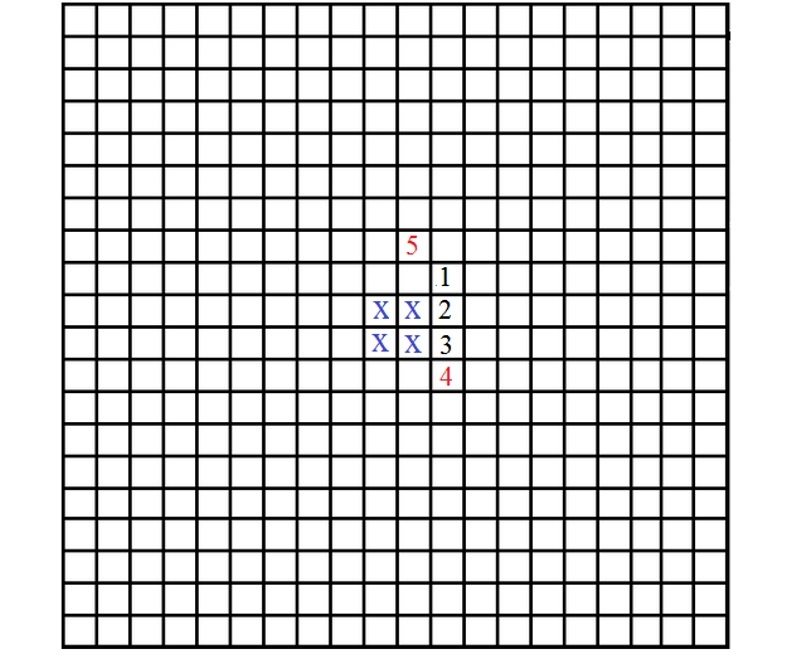
Оказывается, к любой затравке можно добавить лишь конечное число новых крестиков (бесконечные затравки мы пока не затрагиваем). Попробуйте это доказать!
Конфигурации, к которым невозможно, не нарушая правил, добавить новые крестики, назовем полными. В противном случае они считаются неполными. Некоторые полные конфигурации, порожденные тетрадой, обладают изящной симметричной структурой (рис. 3 – 6).
